Wind drift - theory vs reality

[Ballisticboy]

Ballistic,... I think on reflection a bullet’s response to crosswind is merely a mix of, and between, a windvane’s supreme efficiency in equalizing pressure on both of its sides, and say, a truck. There is slippage especially in transient conditions and I also think a good deal of variance between different bullets.

The biggest differences between the wind vane and a bullet are that the wind vane is constrained to move in one plane only and the bullet has far poorer dynamic stability. Like any yawing motion on a highly spinning projectile the bullet will describe the classical yaw rosette about the zero yaw position. The diagram shows the first precession cycle in the yaw angle for the 7.62mm bullet example. Each axis is the bullet yaw angle in degrees.



This yaw cycle takes place over the first 15 yards of the trajectory so you can see how the force due to the yaw is not facing any one direction for very long. Thus any lateral deflection will be minute and largely counteracted by movement in the opposite direction. If the yaw is damped the angle will reduce so the initial deflection will not be entirely counteracted but you are unlikely to notice the difference compared to the down wind drift. Different sizes and designs of bullets will give different detailed behaviour but, for well behaved bullets, the total effect should be small.
What the yaw will do and where the dynamic stability has an effect, is in the amount of yaw induced drag which will show up in the measured drag curve shape but may not show up in the BC. However, unless you go shooting in a gale the yaw angle and thus the drag increment should be small.

 

[BronzeArcher]

Much of the data that people want is out there. It’s just not in the form people seem to want.

But what you’re talking about is simply the uncertainty of inputs...

Which is it? Is there data out there validating leaving out a lateral drag component of wind drift? Or has the uncertainty of inputs (wind field along trajectory, etc.) prevented these experiments being done in a manner to validate wind drift predictions with an accuracy of 10% or better?

... not the fundamental idea that mass is mass and you can’t double count it and have your model make sense. If a proposed model isnt compatible with classical physics, it’s wrong and there isn’t any point in testing it. We can’t just say F = 1.1*MA just because shooters say so. I don’t need a test to say that’s wrong.

Of course, but that's not the only way one can end up with wind drift that seems to decrease with mass (for equal drag curves and muzzle velocities). For example, what if the lateral drift decreases as caliber increases? Since a .338 bullet of given drag curve and muzzle velocity is a lot heavier than smaller caliber bullets, the average shooter may think it is a mass effect.

The 6DOF model is an application of classical physics. Any errors come from factors that have been ignored (there are a few small things that are purposefully neglected) ...

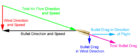
Right, and one thing that has been purposefully neglected is any component of wind drift arising from lateral drag. The justification of this choice is the main point of physics in this discussion.

Totally agree it’s a tiny fraction. But any value more than zero might help explain why identical BC bullets drift slightly differently. Also agree that it will want to weathervane into wind. Problem there is that its momentum toward aimpont dictates, so weathervanibg turns it slightly broadside and this is where the shape other than its “front” would matter.

Yep.

Let's develop the hypothesis of an additional lateral component of wind drift, arising not from the drag along the bullet direction, but from the drag force lateral to the bullet (sideways). The question is not whether this force is zero, but whether it is small enough to be neglected for small arms projectiles and still have predictions accurate to 10% or better.

This force should be proportional to the cross sectional lateral area, call it A, as well as the lateral drag coefficient. There are other terms, but let's focus on these. This additional force will create an additional lateral acceleration that will be the lateral force divided by the bullet mass. So the additional lateral acceleration will proportional to: A/m.

Now let's consider how this term scales with caliber, or bullet diameter, d. If we consider two bullets that are identical in shape and density but have different diameters, then the lateral cross sectional area scales as d^2, and the mass scales as d^3. So the additional lateral acceleration scales as A/m = d^2/d^3 = 1/d.

This is the important prediction of our hypothesis of an additional component to the lateral force: The additional wind drift (acceleration) due to the additional lateral force scales as 1/d. It is smaller for larger caliber bullets than for smaller caliber bullets. Astute observers will notice that the quantity in play here is really a lateral sectional density. The hypothesis can also be stated something like "wind drift will decrease as lateral sectional density increases, other factors being equal."

One point to consider relative to this hypothesis is whether data from wind drift experiments for much larger projectiles (artillery, etc.) would be sufficient to disprove this hypothesis for small arms projectiles, since their diameters are much larger. Neglecting a 1/d effect for artillery may well be valid, even if neglecting the effect for small arms is not.

Something like a simultaneous firing experiment suggested by Keith would shed light on this hypothesis.

 

[davidjoe]

So to the question of whether crosswind can see a bullet’s profile, even a little bit of it, such that different profiles could account at least partly, for different wind drift, I think so. I’d intuit our small arms bullets straddle a middle ground between an archer’s arrow and artillery shells of their same basic shape.

An archer’s arrow, like a wind vane, will quickly turn into a crosswind trying to equalize pressure on the sides of its vanes. Then it will move with the mass of air while persisting forward. If you shot one into a pure crosswind off a skyscraper it would have time to turn completely into the wind, while still moving away from you, sideways.

Our bullets are more belligerent to wind, and artillery shells moreso. Indeed the perfect long range bullet could slip unaffected past 300 yards of aberrant wind in the middle of the 1000 yard range. To be perfect, it would have to transition slowly or not at all into that “facing” the wind mode discussed, where it then travels with the mass. And of course this is not impossible, - a 16 inch naval round’s angular shift from the same 300 yards of aberrant wind would be relatively nil to our bullets, weighing 1/80,000 as much.

I would posit that anytime along a bullet’s path the lateral pressure is not exactly equal in all directions around it, at least some of its profile is “visible” to cross-moving wind that is moving from high to low pressure to try to equalize it. If so, there’s physical interaction, and if there is, shape (other than the front) would indeed matter.

We know that if there’s any wind at all, it will certainly vary over the course of 1/2 mile. So a bullet could vacillate between left and right, up and down. While it’s transitioning, (which is just less of “refusing to transition,” like a semitrailer that starts a roll in a cross sheer that overturns the truck pulling it) the side is being “seen” by the wind.

 

[dcali]

Which is it? Is there data out there validating leaving out a lateral drag component of wind drift? Or has the uncertainty of inputs (wind field along trajectory, etc.) prevented these experiments being done in a manner to validate wind drift predictions with an accuracy of 10% or better

Of course, but that's not the only way one can end up with wind drift that seems to decrease with mass (for equal drag curves and muzzle velocities). For example, what if the lateral drift decreases as caliber increases? Since a .338 bullet of given drag curve and muzzle velocity is a lot heavier than smaller caliber bullets, the average shooter may think it is a mass effect.

Right, and one thing that has been purposefully neglected is any component of wind drift arising from lateral drag. The justification of this choice is the main point of physics in this discussion.

I hear what you're saying, but this has already been done and accounted for. The point mass model does do some hand waving when it comes to rotational effects, but it still works.

This may sound pedantic, but it's important to get the terminology right. There is no lateral drag component. Drag is defined as a force opposite the direction of motion. What there is, and what is taken into account by the 6DOF model, is the relationship between yaw and drag. Another coefficient - CDa is introduced to the model. The total drag coefficient (CD) is a combination of CD0 (zero yaw drag coefficient) and CDa (the yaw drag coefficient). The force always points in the direction opposite of motion, though - there is no lateral force by definition. In this way, 6DOF will calculate the total drag at every step in the trajectory, fully accounting for variation in yaw. The downside is you now have to measure CD0 AND CDa (and a bunch of other stuff), or you can't do it.

Any lateral force is lift, and a totally different discussion with totally different coefficients. The confusion comes from the fact that yaw induces lift and increased drag at the same time. But lift is not responsible for wind. Drag is. (And neither has one whit to do with mass).

The point mass method does not account for rotation an so does not explicitly use CDa - it uses only the total CD. But because of the way we typically measure BCs, CDa doesn't matter - it's all wrapped up in the total drag curve (CD). And the contribution of CDa to CD is small under sane conditions anyhow (that's why we spin the bullets).

The net result is that the point mass method works pretty well under normal conditions and in totality does account for yaw induced drag.

None of this is in any way linked to mass. Drag coefficients are purposefully extracted away from other factors so we don't have to worry about them. Drag force is dependent on CD, area, velocity, and air density. That's it. Mass is simply not a factor. We figure out the drag force (F), the force of gravity (also F), apply them to the bullet's mass (M), and we get a trajectory (A). It's just F = MA.

It's much simpler that way, and it allows you to see what does and doesn't matter very quickly - often without further testing. We do not need further testing to see that mass is already accounted for in the BC, and attributing any drag to mass is not sound physics. Decades of research and thought and testing has led us to isolate various aerodynamic coefficients from each other for exactly this reason - to make the models generally applicable predictors.

 

[davidjoe]

Some models may assume a projectile simply turns into the wind and then moves with the mass, ending that consideration. Thankfully our bullets fight that tendency, very well, or else in say a 10 mph crosswind, they would match the the wind’s travel, foot for foot, like when leading a moving target. According to the charts and experience, they drift only a fraction of distance covered by the mass of air they have travelled through. And their ability to resist that lateral force differs with every specific nuance in design. Perhaps that’s why there isn’t a readily identifiable formula to express what we are terming lateral drag, or the effect of the profile of the of bullet in wind.

 

[davidjoe]

Bronze and OP- as to weight of projectile, down at small end where they all clump together within an order of magnitude, we still have suspicions that given equal BC and velocity, more weight seems to produce less drift. Why is the question. But agree to the thought. Consider the hohum shape of a WWII 16 inch round at 2,800 MV, basically a giant 168 30 cal. At best. Yet range is 30 miles.

 

[243Mendoza]

according to Vaughn in "Rifle Accuracy Facts":
'it takes less than one fast precession cycle for the bullet to align itself to the relative wind vector and reduce the angle of attack due to the wind to near zero."

 

[Ballisticboy]

according to Vaughn in "Rifle Accuracy Facts":
'it takes less than one fast precession cycle for the bullet to align itself to the relative wind vector and reduce the angle of attack due to the wind to near zero."

That would be in the first 15 yards for the 7.62mm bullet I was using as an example. That would also be a complete cycle with any lift force acting in all directions, not just one, so the net effect would be close to zero.

 

[davidjoe]

When I look at my JBM input data sheets for a 10 mph crosswind, we can convert that to 14.7 feet per second. My particular load needs 1.299 seconds to traverse 1,000 yards. I calculate that a 10 mph crosswind has traveled 19.1 feet while my bullet was in flight. The sheet tells me that my windage is 48 inches, for my high BC bullet. I don’t know if it’s proper to describe my bullet as “slippery” or wind “cheating”, but it is definitely not locking itself into the wind’s lateral movement early on.

The bullet is definitely drifting at a faster rate as it goes. Half of the drift occurs between 800 and 1,000 yards, in what is only the last .3 seconds of its flight.

This JBM data is reliable, I do believe. The implication in the two posts above would be that there is not much difference between how all bullets drift in the wind, specifically they all quickly align their path to the wind vector. But if this is the whole story, why does drift rate between competing designs vary so much.

I think the “alignment” principle referenced is indeed a physical tendency, but just like the pull of gravity on all objects does not mean all shapes and densities of objects reach the same terminal velocity, different bullets resist aligning themselves with the wind vector better than others.

 

[Ballisticboy]

When I look at my JBM input data sheets for a 10 mph crosswind, we can convert that to 14.7 feet per second. My particular load needs 1.299 seconds to traverse 1,000 yards. I calculate that a 10 mph crosswind has traveled 19.1 feet while my bullet was in flight. The sheet tells me that my windage is 48 inches, for my high BC bullet. I don’t know if it’s proper to describe my bullet as “slippery” or wind “cheating”, but it is definitely not locking itself into the wind’s lateral movement early on.

Apart from being one factor in the air flow total angle to the direction of travel of the bullet the distance the wind travels during your bullet flight and the wind speed has nothing to do with your down wind drift. Your bullet is not slippery or wind cheating it is just doing everything any bullet, shell or any other projectile will do which is to react to the force being applied to it in the down wind direction. Once the bullet is stabilised into pointing into the total air flow direction then there is no flow to produce anything other than drag. When the bullet is correcting its yaw and moving to point into the air flow then there is flow at an angle to the bullet but it is producing a normal force and moment on the projectile governed by the size of the yaw angle. It is not a lateral drag force unless your bullet is going sideways to the flow in which case you have a lot more than wind drift to worry about. The gyroscopic response to the normal force and moment is to cause the bullet to precess as shown earlier which makes any net lateral acceleration negligible. All the six degree of freedom models that I am aware of calculate the total normal or lift force size, direction and moment about the centre of gravity using coefficients for all the static and dynamic components. They do not ignore certain components unless it is a very poor six degree of freedom model.
As for projectile size the reduced wind response of large projectiles compared to small ones is purely down to the fact that, as said before, the projectile drag force increases with D squared where as the mass increases with D cubed hence from the equation F=MA the lateral acceleration will become less as the calibre increases as M increases faster than F. Large calibre projectiles still have problems with wind, it is one of the largest components in the error budget for a 155mm shell.

 

[dcali]

When I look at my JBM input data sheets for a 10 mph crosswind, we can convert that to 14.7 feet per second. My particular load needs 1.299 seconds to traverse 1,000 yards. I calculate that a 10 mph crosswind has traveled 19.1 feet while my bullet was in flight. The sheet tells me that my windage is 48 inches, for my high BC bullet. I don’t know if it’s proper to describe my bullet as “slippery” or wind “cheating”, but it is definitely not locking itself into the wind’s lateral movement early on.

The bullet is definitely drifting at a faster rate as it goes. Half of the drift occurs between 800 and 1,000 yards, in what is only the last .3 seconds of its flight.

This JBM data is reliable, I do believe. The implication in the two posts above would be that there is not much difference between how all bullets drift in the wind, specifically they all quickly align their path to the wind vector. But if this is the whole story, why does drift rate between competing designs vary so much.

I think the “alignment” principle referenced is indeed a physical tendency, but just like the pull of gravity on all objects does not mean all shapes and densities of objects reach the same terminal velocity, different bullets resist aligning themselves with the wind vector better than others.

You are correct in that the bullet does not move “locked” to the wind. Because the bullet is oriented into the airflow (not pointed in the direction of its motion), the only relevant forces are going to be drag and gravity.

Since the bullet is tipped to the side relative to the shooter, some of that drag force is going to decelerate the bullet along the shooter’s line of sight, and some is going to accelerate it sideways. That is why wind deflection is nonlinear - it increases dramatically with range because the sideways component of drag is accelerating the bullet sideways. The more time it has the do that, the faster the bullet will go. By sideways here, I mean relative to the shooter, not the bullet.

Different bullets of the same weight respond differently to wind because they have different drag characteristics - they have different BCs.

 

[davidjoe]

I’ve followed the wind vector principle. Orientation to total flow is seen in the fact that a flag on a diplomat’s limousine is never blowing exactly straight back unless there is a perfect headwind, and that the faster you drive forward, the closer it gets to straight back whenever there not pure headwind. Check.

A perfect tail/headwind is also the only condition where pressure is equal on the sides of that car, otherwise one must steer, against even a slight angle change. It eludes me that if bullets find this equal pressure almost immediately, as asserted, they aren’t expected to travel nearly the same lateral distance that the host air mass did, while they were in flight. “Equal” pressure is not a flexible concept. (Equal pressure is what you have when a raft is is floating 1 mph on a 1mph river current, with an 1mph breeze the same way, - the raft and water next to it arrive together downstream.) It seems to me that the pressure was necessarily merely “approaching” equilibrium during flight, (as the bullet resisted change) to explain the difference. (I’m all ears on this.) And differing wind sheers the length of a range would compound the delta.

The other question here in these posts is whether the side of the bullet is ever at least partially seen by the wind, to possibly explain why even bullets of different calibers with the same BC seem to respond (drift) differently in the wind.

I’ll again refer to a car, my long Yukon. I know with certainty that if I hit a quartering wind equal to my forward speed, the side of the car experiences some push, not just the front. Just lower all the windows to see that wind blows in one side and out the other. The wind is seeing the side of the car.

If I were driving with my hands off the wheel, this car might center itself into shallow angle wind, or it might turn down wind, but either way once it is centered it wants stay there. The tall sides helped it center. Logic dictates that if I didn’t want a car to easily “find center” in every mild wind, but rather to proceed in a straighter line, a different car might be the answer. Arguably we don’t want our bullets to quickly transition into every moving air mass and move along with it, like a flag does, but to resist them.

My thought’s point is that profile shape, to my thinking might play some significant role at all times there is a transition, especially, which may be nearly all the time of nearly every shot, if pressure is indeed only “approaching” equilibrium during flight rather than reaching it.

 

[Ballisticboy]

The reason your car does not turn into the wind is because it is attached to the ground, a bullet is not. Forget about cars, bikes trucks, houses etc they are not relevant.

 

[davidjoe]

The reason your car does not turn into the wind is because it is attached to the ground, a bullet is not. Forget about cars, bikes trucks, houses etc they are not relevant.

Well agree to disagree on relevancy in the context I used each. Take your hands off the wheel at speed and observe that the wind will of course turn your car. Not trying to be smart here, I don’t know all these answers, especially this one:

Specifically though, why does an average bullet travel 1/4 the lateral distance that the wind did, if it truly equalized pressure and followed the wind vector after some 15 yards? Aren’t those vector arrows supposed to require that it does? Any slippage during the time of its flight means by definition, pressure wasn’t equalized, I would think.

Pressure on both sides of an object that is traversing a current (wind counts) is surely equalized when it is fully adrift. As to before that time, perhaps pressure is merely moving toward equalization. In my raft example, the shape of the raft ceases to matter once it’s moving exactly with the current around it.

I’m suggesting that if a bullet truly sees no side wind whatsoever after say 15 yards, then pressure on both sides would be identical and the bullet is net stationary as to the lateral component of the crosswind. Since in actuality it doesn’t drift nearly that far at all, there must have been a pressure gradient. Since front pressure alone cannot push a bullet to its left or right, there is something else. Gradients always try to equalize, so the gradient would necessitate contact of two materials moving against each other, (air and bullet) and if the front contact cannot explain it, that leaves the sides, which would invoke the shape of the bullet’s profile as at least a factor in drift.

 

[dcali]

The simplest way to put it is that the bullet is exposed to two forces for the purposes of this discussion. One is gravity and not relevant to wind. The other is drag. Drag points opposite the direction of the airflow because that’s what stabilized bullets do. They point into the air flow.

Because the airflow is at an angle when wind is present, the drag force is also at an angle. And since it’s at an angle, you can break it into two perpendicular components - one pointed backwards along the line of sight. The other is much smaller and pointed to 3 or 9 o’clock.

It’s that second component of the drag force that is responsible for accelerating the bullet sideways - wind defection.

Drag is all that matters. There is no “wind on the side of the bullet”. Only air flow along its axis. Any lift forces are small and tend to offset each other as the bullet spins - they are not the cause of wind deflection.

 

[davidjoe]

The simplest way to put it is that the bullet is exposed to two forces for the purposes of this discussion. One is gravity and not relevant to wind. The other is drag. Drag points opposite the direction of the airflow because that’s what stabilized bullets do. They point into the air flow.

Because the airflow is at an angle when wind is present, the drag force is also at an angle. And since it’s at an angle, you can break it into two perpendicular components - one pointed backwards along the line of sight. The other is much smaller and pointed to 3 or 9 o’clock.

It’s that second component of the drag force that is responsible for accelerating the bullet sideways - wind defection.

Drag is all that matters. There is no “wind on the side of the bullet”. Only air flow along its axis. Any lift forces are small and tend to offset each other as the bullet spins - they are not the cause of wind deflection.

I have only seen it described that the bullet aligns with the wind vector, sees no lateral wind, and the moves with mass. I have not read of a perpendicular drag component.

That the bullet does not in fact come close to matching the lateral movement of the airmass seems inconsistent with it achieving zero pressure side to side.

 

[Ballisticboy]

This is a diagram created some time ago to explain the direction in which a stable bullet points in a cross wind.


Remember the only air flow the bullet sees is the total air flow. It does not see two separate air flows.

This diagram tries to show the force which causes wind deflection. I hope it helps understanding.

 

[Crosshair1]

Relative to the bullet there is only one vector and that is the drag force along its centre axis.
Relative to the gun this vector can be broken into a decelerating force along the barrel axis and a deflecting force perpindicular to the barrel (wind)

 

[davidjoe]

I appreciate the illustrations. Will contemplate them.

If the bullet squares itself perfectly with the total airflow, (vector) and sees only a headwind, then it should not gain on, nor lose lateral ground with that mass of air, over the flight time, right? Because nothing is pushing it left or right. Because it is perfectly squared into that headwind and the whole mass of air, say a mile by mile, which includes it, is uniformly moving. It’s as if the bullet is going through still air, just a little more of it.

But they do lose ground with the wind, always and by a huge preponderance. Which is good because it is the tendency that we actually do want them to have for target shooting.

Is the fact that they succumb to the wind not linearly, but at a greatly increasing rate, (see drift chart) analogous to pushing a raft from the bank perpendicular to a river, and watching it lose forward momentum and finally drift exactly in step with the current? If so, that is a very imperfect, drawn out transition. Which is what I postulate bullets undergo. The pushed raft experiences pressure on its upstream side, not just the front, and forms eddies opposite, until it is completely adrift. (This is an analogy, and pushing a raft to a fixed point across a river is not only a classic vector lesson, but also what we are doing with bullets at long range.)

 

[dcali]

Forget about moving with the air or "cutting through it". The interaction of the air with the bullet is the source of the drag force. So you can think about it as if the air isn't there - it's been replaced by a force that is both slowing the bullet down along it's flight path, and pushing it to the side.

And for anyone wondering why we still see round holes with the bullet tipped to the side like that, it's because the angle is tiny - less than 1 degree.