All,
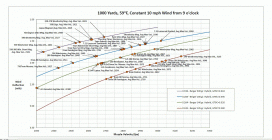
Bryan's approach in his book is to minimize the "non-deterministic" variables of shooting, the most important being wind deflection. He shows that a bullet's wind deflection is directly proportional to lag time, and lag time is determined by a bullet's MV and BC.
I've graphed the bullet curves of 4 Berger hybrids, 0.338, 7mm, 6.5mm, and 6mm in a steady 10mph wind. Using the "Applied Ballistics" online calculator one can find wind deflection directly for each bullet. The average maximum MV's of different cartridges were also placed on the curves to show their relation to each other.
The chart can be used to get a feel for "lag time equivalents". Points on the same horizontal have the same wind penetration ability, regardless of weight and caliper!!! I think this is a good approach for finding equipment that minimizes lag time/wind deflection, regardless of caliper. The Y-axis was inverted so the more north you go on the graph, the lower the wind deflection.
NOTE: The chart says nothing of bullet stability, barrel wear, etc. Also, the MV cartridge values shown are AVERAGES of the Max MVs of all the different powders shown in the Berger reloading manual and may be much lower than what you are getting with your personal loads. They are better used as a relative guide. If you know the MV of your own rifle, just place it on the bullet curve and see where it lands.
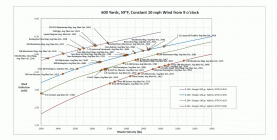
Bryan's approach in his book is to minimize the "non-deterministic" variables of shooting, the most important being wind deflection. He shows that a bullet's wind deflection is directly proportional to lag time, and lag time is determined by a bullet's MV and BC.
I've graphed the bullet curves of 4 Berger hybrids, 0.338, 7mm, 6.5mm, and 6mm in a steady 10mph wind. Using the "Applied Ballistics" online calculator one can find wind deflection directly for each bullet. The average maximum MV's of different cartridges were also placed on the curves to show their relation to each other.
The chart can be used to get a feel for "lag time equivalents". Points on the same horizontal have the same wind penetration ability, regardless of weight and caliper!!! I think this is a good approach for finding equipment that minimizes lag time/wind deflection, regardless of caliper. The Y-axis was inverted so the more north you go on the graph, the lower the wind deflection.
NOTE: The chart says nothing of bullet stability, barrel wear, etc. Also, the MV cartridge values shown are AVERAGES of the Max MVs of all the different powders shown in the Berger reloading manual and may be much lower than what you are getting with your personal loads. They are better used as a relative guide. If you know the MV of your own rifle, just place it on the bullet curve and see where it lands.