222Jim
Silver $$ Contributor
I've measured case weights and volumes using plugs; no statistical difference. i.e. the spent primer weight-to-weight variation is statistically insignificant.Just because the different brands doesn't matter, the math is the same as the exterior dimensions are the same.
No, not saying they are incorrect at all. In fact, they still support the hypotheses for the correlation between weight and case volume. Though I don't have the actual raw data to draw the slope, I can still draw an estimated slope of those data points where you can see the relationship for weight and volume.
And BTW, it would have been better data had the weights no include the primers as the primers have some variance too; as well as the data being a small set.
View attachment 1685808
View attachment 1685809
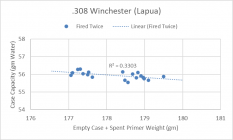
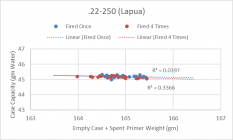
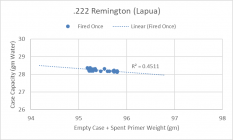
Here are my plots showing the trend line and the "R-Squared". The R-Squared is a statistical calculation that determines how good the data correlates. A value of 1.0 is a perfect correlation and 0.0 means there's absolutely no correlation. For reference, in soft sciences like social sciences, a value of 0.2 - 0.4 is considered good. In pure sciences, a value of 0.6 is considered good. The R-Squared results I got are too small to indicate any correlations between case + spent primer weight and case capacity.
I have a lot more data, including on Nosler cases, but it all led me down the same pathway...........there isn't a statistical correlation between weights and capacities.