I don't think there is anything wrong with using statistics in what we do, but it must be used appropriately and correctly. So it must first be acknowledged that everything we do in shooting is
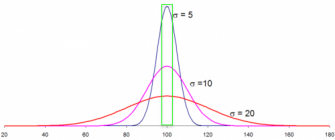
heavily biased toward shooting small. For that reason, the normal distribution we're really dealing with would be analogous to the tall thin [blue] curve shown in the image below:
View attachment 1442485
Note that the standard deviation of this curve corresponds to sigma = 5. In other words, deviation about the mean is far less on average than for the other two curves with larger standard deviations. Another way of stating this would be to say that the values under the blue curve are all much closer on average to the mean value (100). Also note that all three curves have the exact same total area, and that they all use the exact same units on the x-axis.
What these curves mean can be explained as follows. I added the green box around the mean value (i.e. 100) to represent some "acceptable" value a shooter might want or be looking for. For example, it might represent group size, it might represent velocity, it might represent case volume, or something else entirely. What we are looking for as illustrated by the green box is
some set of values that are acceptably close to the mean, meaning they have minimal deviation from the mean.
The key here is that the area of the green box only represents about 10% of the total area under the [red] sigma = 20 curve, about 20% of the area under the [pink] sigma = 10 curve, and about 40% of the area under the [blue] sigma = 5 curve. In other words, when you have a distribution that is biased such that the values in it do not deviate far from the mean (i.e. tall and narrow), by definition any interval selected on the x-axis will represent a much larger area under the curve than it would for a distribution that has significant variance from the mean (i.e. short and wide). Even though the width of the green box equals the same number of units for all three curves, it occupies 40% of the area under the tall narrow [blue] distribution curve, which is
double the area of the green box under the pink curve and
four times the area of the green box under the red curve.
It should not be surprising that a much greater percentage of values in the tall and narrow distribution would fall into the [green] "acceptable" box. Likewise, it shouldn't be difficult to envision why a smaller number of values might be sufficient to generate a high degree of confidence. In contrast, a distribution where variance about the mean is large, thus generating a curve that is wide and short, would require a greater number of values tested to obtain a similar number of "acceptable" values (i.e. those in the green box).
Everything we do is aimed at shooting small. As such we have biased the resulting distribution(s) to have a much narrower standard deviation than might otherwise be expected from a completely random process. The result of that follows statistics perfectly and is clearly demonstrated by the [blue] tall and narrow distribution curve. There's nothing wrong with usaing statistics in shooting, but it has to be applied correctly and the assumptions under which it is used must be valid.
Along this line of reasoning, I typically shoot 3-shot groups for seating depth. I can't "accidentally" stack 3 up in the same hole with a sub-optimal seating depth. Nor is the wind going to fortuitously blow one of the shots back into the group. Those things just don't happen, ever. Further, if I were to use 10-shot groups instead, I would simply be measuring "me", not the load. I don't personally care how many shots anyone uses for group size, or for anything else, because I really don't have any stake in someone else's shooting, only my own. But it does get old when people spout "statistics values" about how many shots it takes to know this or that, which are usually completely off for the reason that everything we do is so heavily biased toward shooting small. So I get Alex's frustration, and I believe the reasons I outlined above are why what we do may sometimes seem not to necessarily obey statistics, even though it really does.