Experimental proof that LC09 brass weight is correlated to case volume.

[jlow]

Have been a bit disappointed not to see any data to address this issue and so set out to find an answer.

The results you see below is the sum total of two separate experiments conducted on two separate days each experiment using 10 pieces of brass. The brass used here is Lake City LC09 twice fired (by me) 223 brass that has been cleaned with SS media, FLR, neck turned, trimmed, deburred, chamfered, primer hole deburred and uniformed. A fired primer was installed and the brass was weighted with a GemPro 250 digital balance. The equipment used in the experiment can be seen in the photo.

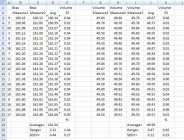
Statistics associated with the brass is in the spreadsheet on the left. The first column is the number identifier associated with each piece of brass i.e. Number 1 would be the first piece of brass I tested. Each piece of brass was weight two times (Brass Measure 1 & Brass Measure 2). The reason the identifier numbers look random is because all the data has been sorted as a function of the average weight of the brass. The reproducible of the balance is can be seen in the two values obtained in the two separate weighing. The numbers are either identical or off by a maximum of 0.06gr.

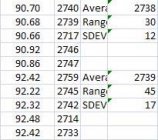
Their average weight for each piece of brass is calculated and displayed under the “Avg” column. Average overall weight was 94.48 gr with a range (ES) of 1.57 gr and a Standard Deviation (SDEV) of 0.49 gr. The range variance as expressed as percentage of average weight was 1.66% and SDEV as a percentage of average weight was 0.51%.

The tend of the variance of the LC brass can be seen in the first bar graph on the left. Interestingly there does not appear to be any particular weight that the cases gravitate towards or away from. When I sorted the data by the average brass weight and plotted it, I got a linear distribution of weights.

Next, I put each piece of brass on the balance and zero the balance. Using a color applicator (for hair - see photo), the case was partially filled with 70% isopropyl alcohol with the last part filled using the 1mL tuberculin syringe with a fine 27 gauge needle. Small volumes of alcohol was added to the case to achieve a flat meniscus. As it turns out, it was pretty easy to figure out when this happens as when the surface was either concave and convex an overhead fluorescence light reflection was visible. It disappeared when the surface was flat. Each piece of brass was filled three times and the final weighs recorded (Volume Measure 1, 2, & 3).

The average weight for each piece was calculated and ES for the three weighting calculated. As can be seen, the method worked pretty well as ES varied between 0.00 to 0.10 gr. Average overall volume was 26.80 gr with a range (ES) of 0.24 gr and a Standard Deviation (SDEV) of 0.06 gr. The range variance as expressed as percentage of average volume was 0.09% and SDEV as a percentage of average volume was 0.24%.
The tend of the variance of the amount of alcohol to fill the brass can be seen in the second graph on the right. There appears to be a linear distribution of the volumes.

Lastly, the average weight for each piece of brass was plotted against the average weight of alcohol needed to fill the same case. This is plotted in the third graph. As can be seen, there is a linear negative correlation between the two numbers i.e. the heavier the piece of brass, the less volume of alcohol it could hold. This makes sense as since the cases have been FLR, their external dimensions should be almost the same, so more brass means that it will take up more of the internal volume.

I calculated the Correlation Coefficient (R) between the two numbers. This is a statistical value that tells you how good the correlation between the two numbers. A perfect correlation gives a value of 1 or -1 (depending on positive or negative correlation), and a value of “0” means there is absolutely no correlation. The value I got from the results of the two separate experiments from two separate days was -0.85 which means that is an excellent correlation.

So in conclusion, a heavier piece of LC09 bras will hold less water, the amount of water it hold is negatively correlated to how heavy the brass is. What this means is it is at least for LC09 brass, it is not necessary to sort them by their volume but weighting them works just as well. You should of course know that this data only applies for LC09 brass and whether it works for other cases remains to be determined.

 

[bheadboy]

Excellent info, from my less formal experience, i have tried the volume measure to sort, and the weight sorting of fired, trimmed brass, and settled on the dry weight sorting as being all i needed.

The times i do use the volume measuring as you outlined, is when i go to a new chambering, standard or AI or other wildcat, to determine case "water volume" for comparison to work up loads. ie tight chambers standard, AI vs factory, wild cat vs known chamberings.

in these cases i find the volume measure very helpful in starting loads and expected results to look for from the round particularly the AI and wildcat versions.

Bob

 

[XTR]

[list type=decimal]
[*]OK, but how much difference does it make on paper
[*]I'd love to see you do this with new WW 308 brass, I'm pretty sure it will completely screw up your data as much of the weight variation is due to the variations in the extractor ring cuts.
[/list]

 

[jlow]

Bheadboy – thanks for your kind comments.

XTR – I am not here to convince anyone of anything, just sharing information that hopefully will help someone with the same questions I have. Also not here to do work for someone else as I have enough on my plate as it is.

If you are a serious shooter, you will have all the tools to do this and what you don’t have can be purchase for less than $5. I understand your skepticism but if you are really interested in the answers, do the experiment and prove to yourself in your system whether it makes a difference. This is the only way I have found to get ahead in precision shooting.

 

[Michael Courtney]

Nice experiment. Thanks for sharing.

 

[LIUNA]

Good Work. Thanks,

 

[Rtheurer]

Ha! its funny sometimes on how these things shake out. I did the exact same test with 100 pcs of Hornady Brass in 6.5X284 and there was NO cooralation to weght of mass to internal volume of fired case. So in effect I found the exact opposite to be in my testing to what youfound in the 10 LC09 cases.
Go figure.

Good post either way. But Im still not convinced there is a direct relation... at least with the larger cases anyway.

Good Job JLOW

RussT

 

[jlow]

Michael & Liuna – glad to be able to share.

Rtheurer – Yes, the data is specific for LC09 brass, for any other brass, one will need to do the experiment to be sure.

One correction is that my experiment was done 2 times each with 10 pieces of brass, so the total N size is actually 20. Not sure why you did not see the correlation with the Hornady brass; could be something else going on in there but I also do not know the scale you are using. As can be seen in my data, the ES differential for the alcohol volume is only 0.24 gr for the 20 pieces of brass and so this is a no go experiment with a scale that can only read down to 0.1 gr. My scale is good down to about 0.02 gr; perhaps this is the reason why it has been difficult to get this correlation in the past.

Even though the variance in volume in my test is not large, yesterday I weight sorted the 100 odd pieces of brass I had previously prep in the same lot. The ES difference in weight for that brass was actually 2.44 gr. Using the ratio of 1.57gr of brass equivalent to 0.24gr of alcohol from my previous experiment; this translates to 0.37gr of alcohol. Using an average case volume of 26.80gr, this translates to about a 1.39% variance in volume between the heaviest and lightest case which is pretty significant.

Not sure if slight difference in case volume will show up in MV but I think if you are shooting a string and have the unfortunate situation where you have included one of the lightest and heaviest case, this 1.39% variance in case volume may translate to significant difference in MV and so vertical stringing in extended distances i.e. 600 yards or greater.

 

[jlow]

Thanks dmoran! Can you give me a bit more description to decipher the data from the graph? I imagine it is something like the numbers is the brass sorted by weight and the color their volume?

Also the question is always the sensitivity of the scale you use.

 

[Rtheurer]

Jlow

I have a Denver instruments Timberline series Lab Balance TP 153, Also has the draft sheild as well. After having a good quality scale its hard to go back to something of lesser qualitity.
In the final discussion point of my project was that I could not see that the lesser mass of brass corralated to lesser internal voulume. My examples did show a typical bell curve as expected for mass weight.While the Internal Volume didn not follow that bell curve and was alot flatter if you will. The large variations in Mass did not prove to be so in internal volume. I wish I had the info on this computer but I digress...no such luck.
This is exactly why I tell people to do there own testing. Prove it to themselves.

OK now lets see what the ES is going to be of your heavy and light cases and how it showes on target. We have done this onthe team machine rest and found not as much varations than you would expect. Hence when I took 600 pieces of loaded match ammo to the world Championships in Australia last year I took it out of the box and loaded it. Same for the bullets.
I think that a small variation in powder is trumped by inconsistant neck tension by far.

Its nice to see that LC09 is that consistant. I have Shot ALOT of that yearbrass in my NRA service rifle. We used it for three years until we ran out.

Again great work Jlow.

RussT

 

[jlow]

Hi,

Thanks guys for chiming in and letting me look at your data.

Donovan, I took the liberty of inputting your data into my spreadsheet which I already made up and here is how it looks:

Your data from the 2nd fired 6Dasher-Lapua brass does not have the degree of correlation that I had with the LC09 brass, but I actually don’t think it looked that bad. I have uploaded both the sheet and the same graphs but now with your data. The bar chart for the case weight has that nice linear shape but the capacity bar chart is also negatively correlated in a linear fashion like mine, there are a few more significant outliers but not too many. When I plotted weight vs. volume, I am still getting a negative correlation between the two with an R value of -0.43. Granted it is not -0.85 but I think you would agree that the two are similar.

The 6Dasher-Lapua brass is bigger and heavier than the LC09 223 and I think part of the problem here is that the bigger the mouth diameter of the neck, the greater the chance for error regardless of skill when making volume measurements. In the laboratory, when we want accurate large volume measurements, we use volumetric flasks like this one which has a narrow neck so that we can adjust the volume accurately at the line in the neck. Having said so, I do believe that there are also likely other factors involved here in terms of why the weight of some pieces of brass is so far off from their predicted volume.

So I think it would be fair to say that in your case, weight does correlate but not 100% and if you need to be 100% sure that you don’t get one of those outlier, using volume determination as you are doing is still the way to go.

Rtheurer – Thanks for your input and kind words. As it turns out, the LC09 brass weight distribution is indeed bell shape i.e. Gaussian distributed. That became obvious when I weight sorted the brass into a fishing tackle box. Most casing gravitated to the middle with lesser number of outliers in the two extreme weigh range. I think the reason I did not see it in my example is because I was using a small sample and not plotting the data in the proper manner – should have been binning them by weight range.

Planning to do some testing for ES next week with the extreme in case weight

 

[Michael Courtney]

Good read. I appreciate everyone sharing their data. I've measured lots of case volumes, but I do my weighing the empty and filled case (with water). I take care to make sure the case is filled level with the top because without due care there can be a concave or convex surface at the top of the water.

Another point of interest is that I have observed that 300 Win Mag cases that have been fired several times (and neck sized) will gain 0.5 to 1.0 grain extra volume capacity after tumbling for three hours in stainless tumbling media. My shot to shot variations in velocity have improved considerably since I began careful cleaning with the stainless tumbling media between firings.

 

[wapiti25]

Thank you for sharing your work.

 

[4xforfun]

Hey D....

Good stuff. You know me...about as scientific minded as my dog... BUT just looking at your printout......you list the brass weight from heavyest to lightest...1-40. The second column lists the case capacity. Just at a glance...the lightest cases have (or should I say trend toward) the highest capacity. Only ONE of the heavier cases hold 41.xx or more, and MOST of the lighter cases hold 41.xx. This is comming from about a three second glance...the extent of my attention span now days!!! It seems to me that there is a trend coralating case weight vs capacity.

What say you??

Are you going to Harris for the state? Dick E.?

Later,
Tod

 

[4xforfun]

What's a "laptop"? ;D

You just poit your car east and pull the trigger..it will find harris.

 

[jlow]

Donovan,

Thanks again for sharing your data with me. You are absolutely right about “the bigger the case, the worse the correlation”. I took some time out and ran the same test on my Win 308 brass that came out of my gas gun, here is the data.

I won’t bore you guys with the details of the technique and analysis again except to say that it is exactly the same as it is for my LC09 223 cases, so read there to get the info. The case weight where as expected was heavier ~160gr with fired primers installed. More of a plateau in terms of case weight distribution and more noise when looking at the case volume. The case weight vs. case volume was still negatively correlated and had an R value of -0.43 which is the same as the 6Dasher-Lapua brass that you tested i.e. R= -0.43, although with a smaller N-size i.e. 20 rounds.

Interestingly, the slope of the line describing weight vs. volume relationship i.e. the “m” from the equation Y=mx +b was -0.113 for the LC09 brass and -0.112 for the Win 308 brass. One can think of the slope as how much unit volume for each unit weight of the brass – how close can you get? LOL!

So the case weight and volume are related, how well depends on caliber and whether you can use this method depends on what you are trying to do and what other work you are willing to put in. I think for extreme accuracy like BR, you should likely stick with case volume, but for less stringent requirements, one might be able to first cull out the poor weight/volume related brass and after that use only weight to bin the brass.

 

[jlow]

Did a small experiment to see if there was any gross difference in MV as a result of differences in brass weight.

Five cases from each end of the weigh spectrum i.e. lightest and heavies LC09 (first column). The rounds were loaded with 77gr Nosler CC, over 24gr of TAC and Rem 7 ½ primer loaded to mag length OAL via ogive =1.900” and fired out of a 20” Stealth. Temp = 74 degrees, humidity = 70%, and barometer = 29inHg. Average MV was almost exactly the same between the two groups and saw only slight difference in ES and SDEV. So it appears at least for LC09 brass under the above conditions, brass weight did not significantly affect MV.

 

[jlow]

Hi Donovan,

Thank you very much for your input. Must say that I am a little surprised that you think the ES is horrible since the SDEV is in the teens which my understanding is reasonably good even though not great. The rounds ended up being sub MOA ~0.69” which although nothing to brag about for a BR gun is probably what one can expect from a factory gun with Lothar Walther barrel (it’s an AR).

However, I would be very happy to be wrong and get some help from you to get me down to even better values. Please tell me more.

 

[jlow]

Hi Donovan,

Perhaps I was not cleared enough in the last post, but as I mentioned already, this is an AR-15 not a benchrest gun and so judging the numbers by that criteria seems to be a bit of apples and oranges?

Sorry I did not give you the info for my chrono, it is a “Shooting Chrony Alpha”, so certainly no “5 separate chronograph”. Barrel heating I tried to minimize by using a 2 min cool down between rounds and I shot the two groups round Robin fashion. Barrel fouling was done using 13 rounds prior to the 10 rounds in question. Tried downloading your file but unfortunately my anti-viral software does not allow me to do it.

You obviousely have better numbers, but perhaps it would also help if you can give us some numbers in terms of what you would consider “reasonable” ES for a AR-15 223. As you have also stated, it would also help me to know your gun setup and the same particulars that you ask me?

 

[kennyg]

So for those of you sorting by volume, what works best to fill the cases with? I see the OP used alcohol. Is this the standard? Thanks for all the great info!