Here is a question I have. Our shooting team captured MV and SD with a Labradar and then also terminal velocity n SD on our ShotMarker. I understand these are two different chrono systems and therefore no real calibration or correlation between them. But, on three different rifles, we see the SDs at 600 yds being lower than SDs at the muzzle. Anyone else see this type of data?
SD Muzzle vs Target
- Thread starter Bob3700
- Start date
Velocity is higher at the muzzle, hence a wider range, at the target the velocity has slowed significantly, hence a narrower velocity range. 1% of 3000 fps =30 at muzzle. 1% of say 2000 fps at target = 20 fps. The percentage should be about the same.
Frank
Frank
memilanuk
Gold $$ Contributor
Frank makes a good point.
Also, the "chrono" feature of the ShotMarker - or any e-target, really - is more of a side effect, and not really a design feature. Generally the manufacturers do not recommend you put too much stock in those numbers, and particularly don't go changing your load based on the "chrono" numbers at the target.
Also, the "chrono" feature of the ShotMarker - or any e-target, really - is more of a side effect, and not really a design feature. Generally the manufacturers do not recommend you put too much stock in those numbers, and particularly don't go changing your load based on the "chrono" numbers at the target.
Does WIND direction and velocity over 600/1000 yards have a more pronounced effect DOWN RANGE on projectile velocity?
Three Garin Xero's, one close, one down range, one spare for the one you shot.
Three Garin Xero's, one close, one down range, one spare for the one you shot.
i have actually shot over an optical pro-chrony placed at 100 yards.... BUT with rimfire. roughly 'correlated' a pair of them first at the muzzle, then moved one downrange. one could always protect the downrange with AR500 plate. however centerfire and 600 yards... hahaha...
i keep the chronys around for use with my archery gear.
You would think that any velocity variation at the muzzle would translate to variation at the target. 30 fps variation at the muzzle would translate to XX fps at the target. How does the variation become less at distance?
Is the bullet flying in a more stable condition at distance than at the muzzle?
Krogen
Gold $$ Contributor
If you only look at this statistically, then textbook standard deviation is proportional to the mean or average value. For example take a random velocity dataset at the muzzle with an average velocity of 3000 fps. Suppose it has a standard deviation of 30 fps. Then, take the same dataset and pretend the velocities at distance are exactly 2/3 the muzzle velocities. The average would be 2000 fps and the standard deviation would be 20 fps. So standard deviation is proportional to average with a scaled dataset.
However . . . . There should be no expectation that the velocity dataset at distance is exactly proportional to the muzzle velocities. There are lots of variables. To name a few: individual ballistic coefficients of each bullet vary, ballistic coefficient varies with velocity, conditions vary from shot to shot and . . . .
Then there's the measurement system differences. For example, use a Garmin at the muzzle and Shotmarker at the target. Garmin is doppler RADAR, while the Shotmarker measures time of flight between two sensors. Those sensors look for the shockwave crossing microphones that only a few inches apart. Shotmarker is unlikely to be as accurate as the Garmin. They're two significantly different measurement systems.
And finally there's the standard deviation calculation itself. Population standard deviation and Sample standard deviation are different. One needs to know what method the measurement device uses or you can get fooled. In Excel, these functions are STDEV.P and STDEV.S if you want to play with datasets.
However . . . . There should be no expectation that the velocity dataset at distance is exactly proportional to the muzzle velocities. There are lots of variables. To name a few: individual ballistic coefficients of each bullet vary, ballistic coefficient varies with velocity, conditions vary from shot to shot and . . . .
Then there's the measurement system differences. For example, use a Garmin at the muzzle and Shotmarker at the target. Garmin is doppler RADAR, while the Shotmarker measures time of flight between two sensors. Those sensors look for the shockwave crossing microphones that only a few inches apart. Shotmarker is unlikely to be as accurate as the Garmin. They're two significantly different measurement systems.
And finally there's the standard deviation calculation itself. Population standard deviation and Sample standard deviation are different. One needs to know what method the measurement device uses or you can get fooled. In Excel, these functions are STDEV.P and STDEV.S if you want to play with datasets.
Bob3700, I was referring to percentage, not actual FPS. The bullet slows down so you have two very different velocities. Using the same variation percentage for each range will result in different actual numbers. This is a generalization. As Krogen mentioned there are a lot of little variations along the way.
Frank
Frank
Average joe
Gold $$ Contributor
I have seen the exact opposite of this….
Usually the velocity spread at the target is much greater than at the muzzle in my limited experience .
I’ve never trusted the velocity indication of the targets.
CharlieNC
Gold $$ Contributor
There is NO statistics or physics reason that SD is always proportional to the mean.
Krogen
Gold $$ Contributor
Wrong!! Do the math. I thought I explained it fairly well. Take a dataset and also one that is scaled to half the velocities and your mean and standard deviation will also be half the original dataset's.
RegionRat
Gold $$ Contributor
Let me see if I can help keep the peace a little.
Charlie is right, but so is Krogen, so please bear with me and I will explain why with an example.
Imagine a perfect set of bullets, all weigh the same and have identical BC, but there is dispersion in muzzle velocity. The day they are shot and tracked all the way to the 1000 yard line, there is no change in the air for the three shots.
This represents a set of bullets on a calm day, where I hope to illustrate the feel of how bullet tracks tend to look statistically at the muzzle, versus down range.
I will use a common Berger 30 cal 175 which happens to be the default case that pops up when you try their ballistic calculator on their web site. It will be used to illustrate the point.
On the left are the muzzle speeds of the three shots. On the right are their speeds at the 1000 yard mark.
You can see how things look by the time they reach the target. By proportion, the stats look smaller to folks when the stars align and the bullets and hardware is classy. So this is the ideal case and it would require lucky winds to make these stat values smaller, but even that has happened.
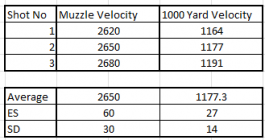
On a good day, with calm winds, the SD/AVG at the muzzle was a ratio of 30/2650 = 0.0113
On that day at the 1000 yard line, the SD/AVG looks like 14/1177.3 = 0.0119
There is lots of room for the wind to add dispersion, and for the BC to vary, and expand the downrange stats to match the muzzle. But when things are classy and winds are calm, it is not rare to see them as above.
So folks, as someone who has been tracking projectiles (both outbound and inbound) for several decades, the stats down range take a little getting used to, but yes the value at the target can be much smaller than the one at the muzzle and it isn't due to ShotMarker error. YMMV
Charlie is right, but so is Krogen, so please bear with me and I will explain why with an example.
Imagine a perfect set of bullets, all weigh the same and have identical BC, but there is dispersion in muzzle velocity. The day they are shot and tracked all the way to the 1000 yard line, there is no change in the air for the three shots.
This represents a set of bullets on a calm day, where I hope to illustrate the feel of how bullet tracks tend to look statistically at the muzzle, versus down range.
I will use a common Berger 30 cal 175 which happens to be the default case that pops up when you try their ballistic calculator on their web site. It will be used to illustrate the point.
On the left are the muzzle speeds of the three shots. On the right are their speeds at the 1000 yard mark.
You can see how things look by the time they reach the target. By proportion, the stats look smaller to folks when the stars align and the bullets and hardware is classy. So this is the ideal case and it would require lucky winds to make these stat values smaller, but even that has happened.
On a good day, with calm winds, the SD/AVG at the muzzle was a ratio of 30/2650 = 0.0113
On that day at the 1000 yard line, the SD/AVG looks like 14/1177.3 = 0.0119
There is lots of room for the wind to add dispersion, and for the BC to vary, and expand the downrange stats to match the muzzle. But when things are classy and winds are calm, it is not rare to see them as above.
So folks, as someone who has been tracking projectiles (both outbound and inbound) for several decades, the stats down range take a little getting used to, but yes the value at the target can be much smaller than the one at the muzzle and it isn't due to ShotMarker error. YMMV
CharlieNC
Gold $$ Contributor
If you simply subtract a constant value from each measurement, the mean is affected according and the SD remains unchanged. One must understand the physics of what is actually happening to know which mathematical approach to utilize.
drop_point
Silver $$ Contributor
Velocity at the muzzle isn't influenced by BC. At 600, BC variation will influence velocity/SD.
CharlieNC
Gold $$ Contributor
Running a ballistic calculator for a 40fps difference in muzzle velocity out to 1000yd, the %decrease is nearly the same for both. And the %ES at each distance is essentially the same as well, which does indicate the %CV = SD/Average would be the same as well. Of course this does not include the effect of differences in BC, etc.
Upgrades & Donations
This Forum's expenses are primarily paid by member contributions. You can upgrade your Forum membership in seconds. Gold and Silver members get unlimited FREE classifieds for one year. Gold members can upload custom avatars.
Click Upgrade Membership Button ABOVE to get Gold or Silver Status.
You can also donate any amount, large or small, with the button below. Include your Forum Name in the PayPal Notes field.
To DONATE by CHECK, or make a recurring donation, CLICK HERE to learn how.
Click Upgrade Membership Button ABOVE to get Gold or Silver Status.
You can also donate any amount, large or small, with the button below. Include your Forum Name in the PayPal Notes field.
To DONATE by CHECK, or make a recurring donation, CLICK HERE to learn how.