You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Coup De Grace measurement... how?
- Thread starter LVLAaron
- Start date
Tucker65
Gold $$ Contributor
Make a tube that is bored to seat up against the barrel shoulder on one end and big enough for the ball to fit in on the other end. Make the tube longer than dimension A. Then you can use a depth mic to measure from the face of the tube to the ball and do the math to come up with dimension A.
Doug Beach
Silver $$ Contributor
Would simply cutting a partial cone, then threading the action on, bolt included, until it stops, work? Then you just measure the gap between receiver face and action face, add your desired clearance, and cut the cone that much deeper. Works on any other cone breech I’ve seen, but I’ve never handled a Coup de Grace.
Rank Amateur
Gold $$ Contributor
Assuming that is the diagram of a barrel chamber/tenon? If so, why not cast the chamber and just measure?
DaveTooley
Gold $$ Contributor
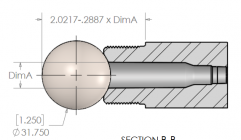
I don't see how A has anything to do with a 1.250" radiused CB. Just an evil engineer.
LVLAaron
Gold $$ Contributor
Would simply cutting a partial cone, then threading the action on, bolt included, until it stops, work? Then you just measure the gap between receiver face and action face, add your desired clearance, and cut the cone that much deeper. Works on any other cone breech I’ve seen, but I’ve never handled a Coup de Grace.
Works great, if you have the action in hand.
LVLAaron
Gold $$ Contributor
I don't see how A has anything to do with a 1.250" radiused CB. Just an evil engineer.
You're right. I'm running on fumes today. I'm looking for the "2.0217-.2887 x DimA" measurement, not DimA.
DaveTooley
Gold $$ Contributor
Do the math. Not much change for a few thou change in A. How are you cutting the radius? Err on the side of more clearance.
Doug Beach
Silver $$ Contributor
Aha. Yes, yes it does.Works great, if you have the action in hand.
DaveTooley
Gold $$ Contributor
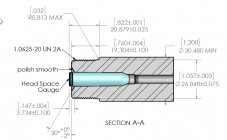
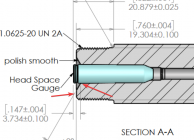
I have kept a 2" travel indicator on every manual machine I've ownedIf you have a DRO on your lathe touch off both surfaces.
DaveTooley
Gold $$ Contributor
.822"-.760= .062"
.147"-.062"= .085" at 30'
Am I missing something
.147"-.062"= .085" at 30'
Am I missing something
When I did my CDG in July, I touched my DTI on the shoulder, zeroed the DRO and a dial ind on the apron, backed the crosslide off, and went to the ball and ran the DTI up on the ball and touched it. Both the DRO and dial ind agreed. As for DIM A, I just used sammi chamber spec for 223, I cut a 223AI chamber. Worked out good. Great action, and I have one more to do a 6Dasher build on.
jackieschmidt
Gold $$ Contributor
This seems like the simple solution.. or at least that’s the way I would do it.Make a tube that is bored to seat up against the barrel shoulder on one end and big enough for the ball to fit in on the other end. Make the tube longer than dimension A. Then you can use a depth mic to measure from the face of the tube to the ball and do the math to come up with dimension A.
WSnyder
Silver $$ Contributor
SameI have kept a 2" travel indicator on every manual machine I've owned
I'm sure you've done many more cone breeches than I can ever even imagine doing, so maybe you have some insight into how to reliably gauge that 0.085 distance. There's no square surface to mic against. I think that's why they supply the gauge ball drawing as well. The ball will seat solidly against the cone and can then be measured by conventional mics..822"-.760= .062"
.147"-.062"= .085" at 30'
Am I missing something
(full disclosure, I just set that barrel on the bench up for photo)
Last edited:
LVLAaron
Gold $$ Contributor
Move in .085 from the face of the breech end... use compound to cut the cone.
The problem with the 1 inch ball bearing method - The ball doesn't make contact with the cone, it rests on edge of the hole... so if there's a chamfer on your chamber... the measurement will be off.
I assume that's why ARC suggests a larger ball... but I'm bad at that kind of math.

The problem with the 1 inch ball bearing method - The ball doesn't make contact with the cone, it rests on edge of the hole... so if there's a chamfer on your chamber... the measurement will be off.
I assume that's why ARC suggests a larger ball... but I'm bad at that kind of math.
Well, the example I showed was for a Panda barrel in 6.5x47, and I did the CAD sketch to make sure that the ball was resting against the breech cone before I did the measurement. I've confirmed it before with some dykem as well, but you are probably correct for the ARC dimensions, hence the 1.25 ball.Move in .085 from the face of the breech end... use compound to cut the cone.
View attachment 1483484
The problem with the 1 inch ball bearing method - The ball doesn't make contact with the cone, it rests on edge of the hole... so if there's a chamfer on your chamber... the measurement will be off.
I assume that's why ARC suggests a larger ball... but I'm bad at that kind of math.
Similar threads
- Replies
- 83
- Views
- 11,145
- Replies
- 1
- Views
- 141
- Replies
- 4
- Views
- 1,130
Upgrades & Donations
This Forum's expenses are primarily paid by member contributions. You can upgrade your Forum membership in seconds. Gold and Silver members get unlimited FREE classifieds for one year. Gold members can upload custom avatars.

Click Upgrade Membership Button ABOVE to get Gold or Silver Status.
You can also donate any amount, large or small, with the button below. Include your Forum Name in the PayPal Notes field.
To DONATE by CHECK, or make a recurring donation, CLICK HERE to learn how.

Click Upgrade Membership Button ABOVE to get Gold or Silver Status.
You can also donate any amount, large or small, with the button below. Include your Forum Name in the PayPal Notes field.
To DONATE by CHECK, or make a recurring donation, CLICK HERE to learn how.