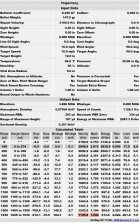
The interesting thing about ballistic drop and drift charts is that they truly don’t need to know bullet weight or diameter. If muzzle velocity and BC are entered, the drop and drift are fixed by those two variables regardless of what shape and weight of bullet was used to arrive at that particular BC. A .500 bc projectile at 2,800 fps, if you accept the principle of BC, drops and drifts the same whether .224, .243, .308 or .338.
For us busy at punching holes near the center, we aren’t concerned with how hard the bullet hits the berm, in fact any kinetic energy that didn’t translate directly to wind-bucking is useless to us, and required unnecessary powder and metal to achieve.
Extra powder that did not reduce drift is costly to us in at least three ways:
1) barrel heat which causes wear and eventually inaccuracy or blowups in long strings;
2) fatigue, even if the recoil is manageable without penalty in group size down range, but because of vibrations it’s actually not possible to achieve accuracy parity;
3) cost, the powder had to be bought, and if more was used for the same drift result, then the bullet was heavier, making it likely to cost more as well.
So if this is all logical, and if it is generally true that getting a light weight bullet up to the same speed as a heavy bullet, is easier, then it follows that what we should truly be concerned with in pursuits such as Fclass, when it comes to BC as an isolated issue, is the ratio between a bullet’s weight and its BC.
I’m hypothesizing that if we simply ignore the decimal point for our bullets, and divide that number by their weight, we get a fairly useful number.
We have heard standout Fclass guys dissuade shooting 6mms in matches for various reasons, though they can win at 600 majors, but why do they garner this spot that is both good, and then bad. There may be a different, bullet-related reason underlying picking on the sixes.
Here are some interesting results looking just at Hornady’s A-Tip line as an example because tipping them is irrelevant.
.308 250:
878 divided 250 = 3.512
7mm
838 divided by 190 = 4.41
Just for fun Berger 195
755 divided by 195 = 3.87
Run this on all the popular big LR bullets of your choice, and a very tight spread emerges. (It also works in comparing the same maker’s options).
Higher numbers are better in this regard. When we move down to 6 mm bullets something very interesting changes, instead of the tight cluster of numbers in the high 3’s and low 4’s we get this:
.243 A-Tip
604 divided by 110 = 5.49
The same drastic departure follows for the DTAC. I believe this quantitative and gross disparity is why 6’s seem to have a certain unarticulated advantage, - they are dramatically higher in BC for their weight, relative to everything else you could select to shoot, especially factoring in the their MV.
For us busy at punching holes near the center, we aren’t concerned with how hard the bullet hits the berm, in fact any kinetic energy that didn’t translate directly to wind-bucking is useless to us, and required unnecessary powder and metal to achieve.
Extra powder that did not reduce drift is costly to us in at least three ways:
1) barrel heat which causes wear and eventually inaccuracy or blowups in long strings;
2) fatigue, even if the recoil is manageable without penalty in group size down range, but because of vibrations it’s actually not possible to achieve accuracy parity;
3) cost, the powder had to be bought, and if more was used for the same drift result, then the bullet was heavier, making it likely to cost more as well.
So if this is all logical, and if it is generally true that getting a light weight bullet up to the same speed as a heavy bullet, is easier, then it follows that what we should truly be concerned with in pursuits such as Fclass, when it comes to BC as an isolated issue, is the ratio between a bullet’s weight and its BC.
I’m hypothesizing that if we simply ignore the decimal point for our bullets, and divide that number by their weight, we get a fairly useful number.
We have heard standout Fclass guys dissuade shooting 6mms in matches for various reasons, though they can win at 600 majors, but why do they garner this spot that is both good, and then bad. There may be a different, bullet-related reason underlying picking on the sixes.
Here are some interesting results looking just at Hornady’s A-Tip line as an example because tipping them is irrelevant.
.308 250:
878 divided 250 = 3.512
7mm
838 divided by 190 = 4.41
Just for fun Berger 195
755 divided by 195 = 3.87
Run this on all the popular big LR bullets of your choice, and a very tight spread emerges. (It also works in comparing the same maker’s options).
Higher numbers are better in this regard. When we move down to 6 mm bullets something very interesting changes, instead of the tight cluster of numbers in the high 3’s and low 4’s we get this:
.243 A-Tip
604 divided by 110 = 5.49
The same drastic departure follows for the DTAC. I believe this quantitative and gross disparity is why 6’s seem to have a certain unarticulated advantage, - they are dramatically higher in BC for their weight, relative to everything else you could select to shoot, especially factoring in the their MV.
Last edited: