Measuring case internal volume

[Boomer79]

What is an efficient way to measure the internal case volume?

 

[Alex Wheeler]

I would like to know as well. I have tried the water method and also using fine gun powder. If I did the same case over I could never get repeatable results. I think the best way would be using a chrono and plotting the shot on paper looking for vertical

 

[jlow]

There really is no efficient (fast) way to measure internal case volume – it’s the nature of the beast, but it is possible to accurately and precisely measure internal case volume. The way I do it is to

1) Use only fired brass with the primer still installed.

2) Put it on a GemPro 250 digital scale and tare the scale.

3) Fill the case to almost to the top of the neck with rubbing alcohol using a 5-ml syringe without a needle.

4) Fill the case to the rim using a 1-ml syringe equipped with a 27gauge needle.

5) Look at the surface of the alcohol solution with a light in the back, you should see the reflection of the light and how flat the surface should be easily visible i.e. you should be able to tell if it is concave, convex, or flat.

6) With the needle of the syringe inserted into the surface, withdraw or inject into the solution until you get a flat surface. A head mounted binocular magnifier will be needed.

7) Read the weight off the scale, that is the volume of the case.

If the solution you use is water, 1 gram = 1 mL but since you are using rubbing alcohol, this stuff will have a slightly different density and that number is slightly off. However for this purpose which is to sort the case relative to volume, you can just use the weight.

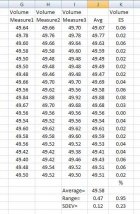
To give you an idea of how good this method is, you can look at the numbers I got for 20 pieces of Win 308 brass I measured back in August. Each case was measured three times (measure 1, measure 2, and measure 3). I calculate their average volume weigh and the ES of the three measurements. The weight unit used here is in grains.

 

[dannyjbiggs]

Boomer...if you want to get through by supper time, why not just weight-sort your cases on a good digital scale and sort to the nearest one-half grain (after neck trimming, flash-hole reaming, primer pocket standardization, etc). I did not see a significant difference when I checked my weight-sorted lots of brass under the former method compared with the traditional water-weight method!

Danny Biggs

 

[Mulligan]

There really is no efficient (fast) way to measure internal case volume – it’s the nature of the beast, but it is possible to accurately and precisely measure internal case volume. The way I do it is to

1) Use only fired brass with the primer still installed.

2) Put it on a GemPro 250 digital scale and tare the scale.

3) Fill the case to almost to the top of the neck with rubbing alcohol using a 5-ml syringe without a needle.

4) Fill the case to the rim using a 1-ml syringe equipped with a 27gauge needle.

5) Look at the surface of the alcohol solution with a light in the back, you should see the reflection of the light and how flat the surface should be easily visible i.e. you should be able to tell if it is concave, convex, or flat.

6) With the needle of the syringe inserted into the surface, withdraw or inject into the solution until you get a flat surface. A head mounted binocular magnifier will be needed.

7) Read the weight off the scale, that is the volume of the case.

If the solution you use is water, 1 gram = 1 mL but since you are using rubbing alcohol, this stuff will have a slightly different density and that number is slightly off. However for this purpose which is to sort the case relative to volume, you can just use the weight.

To give you an idea of how good this method is, you can look at the numbers I got for 20 pieces of Win 308 brass I measured back in August. Each case was measured three times (measure 1, measure 2, and measure 3). I calculate their average volume weigh and the ES of the three measurements. The weight unit used here is in grains.

How would you sort? In other words, which cases would be in the same group?
CW

 

[Tiratore]

I'll probably regret this, but ...

The importance of many reloading variables can be determined by measuring or calculating the related velocity variation. The importance of many others can’t. Case volume is probably one that can, so we can use velocity variation to assess volume’s effect on target performance.


Because of the difficulty in measuring case volume directly (surface tension, bubbles, etc.) by filling cases with a medium such as water with detergent, powder, etc., I submit without proof that weight measurement gives a better indication of volume than direct measurement. The volume of a cartridge case is equal to the chamber volume minus the volume of the metal making up the case and primer, minus the volume of the extractor groove. The density of cartridge brass is a constant, for all practical purposes. Within a brand, the volume of the extractor groove is likewise constant. The variation of volume within a cartridge case (variation, not the actual value) can be determined accurately by weighing representative cartridge cases.


I have measured the weight of 20 VarTarg cases made from several parent cases. For example, weights of cases made from Remington 221 Fireball cases have an average of 82.65 grains, and a standard deviation of 0.33 grains. I have fired cases of different weights and determined the effect of case weight upon muzzle velocity. The standard deviation in velocity corresponding to that case weight distribution is 3.6 fps. A typical standard deviation in velocity seen from ammunition made from such cases is 20 fps, due to all causes including case volume.


It is possible to calculate the contribution of case volume to the total velocity variation from the above data:


The square of the SD of a population’s velocity equals the sum of the squares of the velocity variations due to each of those independent factors that cause velocity variation. SD2 is thus equal to 400. The implied SD due to case weight variation of Remington cases is 3.6, and (3.6)2 = 12.96, and that subtracted from 400 is 387. The square root of that is 19.67. So, the standard deviation of the velocity can be reduced from 20 to 19.67 by removing any variation in case weight. It would seem the sorting by case weight within a batch of cases by one manufacturer has an immeasurably small effect. (apparently exponents don't come through correctly, but you've probably already figured SD2 is supposed to be SD squared, etc.)

 

[savagedasher]

I have a tool I made an I get the same result 10 times all within .01 Gr . It is not total case capacity because is done off the shoulder and a portion of the neck .
The cases must be fired in the gun and un touched when checking . Don't have a problem keeping ES of 5 and under using a charge master . Larry

 

[Mulligan]

I have a tool I made an I get the same result 10 times all within .01 Gr . It is not total case capacity because is done off the shoulder and a portion of the neck .
The cases must be fired in the gun and un touched when checking . Don't have a problem keeping ES of 5 and under using a charge master . Larry

Do tell, what have you built?
CW

 

[savagedasher]

Do tell, what have you built?
CW

Hope to have it in production soon .
6 mm is easy but want to make it for other caliber . Not one for each . Larry

 

[mikecr]

With cartridges & lot to lot brass I've tested I did not see direct correlation between case weights and capacities. So now I only act on H20 capacity.
I fully prep & fire form cases 3 times, neck sizing only, with a final trim, to stable dimensions -as measured. I do my standard vibratory cleaning with primers removed & then air blown out. As far as the flash hole, I used to tare the scale with a case standing on a plastic golf tee(in the flash hole). This worked fine. Now I use this: http://www.xxicsi.com/primer-pocket-plugs.html
Then I slowly fill the case with room temp water using an eyedropper. I had earlier added a few drops of alcohol to the water to reduce surface tension a bit. Once full, I remove the meniscus at the case mouth(to flat) with a tissue corner, and get my weight. A hundred or so cases takes a while to do.

I let QuickLoad tell me acceptable H20 capacity range, and so far I've been culling around ~20% of my cases falling outside the range. At this point I wouldn't care what culled cases themselves weigh, matching or vastly different,, they don't match the mean of H20 capacities within range.
I also do not FL size cases, ever, so my capacities hold well by then.
If I did FL size, especially if leading to more trimming, and annealing, etc., I wouldn't bother trying to match & manage H20 capacities, nor would I act on any more than significant case weight anomalies. Where results from FL sized brass show potential problem cases, I'd just drop em into a brass can at the range. Simple as that.

 

[MrBottleneck]

I sort my Lapua brass by weight.
Then once I fire form I will get my H2O (I use H2O) capacity which I use in QL.
I use these dandy lil syringes my dentist gives me (hes a gun nut). They work perfect for filling the case.
Its approx a 5" long tube .5" in diameter with the perfect size lil nozzle.

 

[savagedasher]

I sort my Lapua brass by weight.
Then once I fire form I will get my H2O (I use H2O) capacity which I use in QL.
I use these dandy lil syringes my dentist gives me (hes a gun nut). They work perfect for filling the case.
Its approx a 5" long tube .5" in diameter with the perfect size lil nozzle.
View attachment 1010036

 

[savagedasher]

I find using water with a dropper you can get within .03 gr repeatedly Better then not doing it .
I get .01 repeatedly With my tool . But it is not totally case capacity . Larry

 

[Tiratore]

 

[M14AMU]

Dam nation! Now I've found a way after 60 years of shooting LR whereby I might can reduce this 10 round group fired from 900 yards to maybe 1 1/2"! Course at 77 years age I'm gonna be all tied up sorting these case internal dimensions out to a degree that I may not have enough time remaining to shoot another group!

308 Win/Remington M700 factory barrel/action by Sharps Man, on Flickr

 

[Ned Ludd]

View attachment 1010066

There's an issue with this graph. Because the outside dimensions of a case are limited by the chamber (with the exception of the extractor groove), as case weight increases, case volume decreases. Any graph plotting case volume versus weight should have a negative slope. This graph has a positive slope. How is that possible?


Determining case volume with water isn't very difficult if you have an accurate balance:

http://forum.accurateshooter.com/threads/case-volume-determination-pic-heavy.3896148/

Here is a recent set of cases for which I measured water volume and prepared a graph. The number of cases was not large (15 total), but is fairly representative of what you will usually find if you carry out the same exercise, which is that there are always a few outliers that can be very far off the trend line of the scatter plot. The negative slope trend line certainly tells you that as case weight increases, volume generally decreases, but the outliers and relatively poor Pearson's R for the trend line also demonstrate that weighing cases will never be a perfect substitute for actually determining case volume. Testing a greater number of cases will certainly improve the fit, but the outliers will always be there.

Although I regularly measure case volume, I'm basically too lazy to determine water volume for more than 10 or 20 cases at a time. For that reason, I sort cases for competition by weight, based on the the fact that the trend line does indeed have a negative slope. I acknowledge and accept the certain presence of outliers within any weight-based sorting method. My general feeling is that even if weight-sorting isn't a "perfect" substitute for determining actual case volume, cases sorted by weight are likely to be much more uniform in volume than by doing nothing at all (i.e. non-sorted cases), even with the presence of outliers. So I sort by weight because it is fast and easy and should give better uniformity than unsorted cases, but acknowledge the caveat of occasional outliers.

 

[normmatzen]

Tiratore,

Brilliant!

I will still measure the volume of a statistical sample of new cases to determine the volume to use in QL. But, I will only measure case weight for ordering the use of the cases! And, if they don't vary too much, I will totally disregard measuring case weight!

Norm

 

[Tiratore]

There's an issue with this graph. Because the outside dimensions of a case are limited by the chamber (with the exception of the extractor groove), as case weight increases, case volume decreases. Any graph plotting case volume versus weight should have a negative slope. This graph has a positive slope. How is that possible?


Determining case volume with water isn't very difficult if you have an accurate balance:

http://forum.accurateshooter.com/threads/case-volume-determination-pic-heavy.3896148/

Here is a recent set of cases for which I measured water volume and prepared a graph. The number of cases was not large (15 total), but is fairly representative of what you will usually find if you carry out the same exercise, which is that there are always a few outliers that can be very far off the trend line of the scatter plot. The negative slope trend line certainly tells you that as case weight increases, volume generally decreases, but the outliers and relatively poor Pearson's R for the trend line also demonstrate that weighing cases will never be a perfect substitute for actually determining case volume. Testing a greater number of cases will certainly improve the fit, but the outliers will always be there.

Although I regularly measure case volume, I'm basically too lazy to determine water volume for more than 10 or 20 cases at a time. For that reason, I sort cases for competition by weight, based on the the fact that the trend line does indeed have a negative slope. I acknowledge and accept the certain presence of outliers within any weight-based sorting method. My general feeling is that even if weight-sorting isn't a "perfect" substitute for determining actual case volume, cases sorted by weight are likely to be much more uniform in volume than by doing nothing at all (i.e. non-sorted cases), even with the presence of outliers. So I sort by weight because it is fast and easy and should give better uniformity than unsorted cases, but acknowledge the caveat of occasional outliers.

My chart is empty weight versus filled weight, not empty weight versus water weight. It is correct. If, alternatively, one would plot case weight versus case-weight-with-water-minus-empty-case-weight, the relationship should be similar to that shown above.

 

[Tiratore]

This is what you were expecting to see -- same data, plus some other populations, but water-only plotted versus case weight.

 

[Ned Ludd]

If case weight falls within a fairly narrow and consistent range, adding the extra weight of water plus the case shouldn't change the slope of the line, only the y-intercept. Case volume will always show the general trend of decreasing as case weight increases. Your first method of plotting the data is misleading with regard to the effect of case weight on case capacity. It's merely a way of making the data look much better than it really is because the critical value, which is the actual water weight or case volume, becomes proportionally reduced when the weight of the case is also included. For example, take the highest (~90 gr) and lowest (~84.7 gr) case weight values. When graphed appropriately to illustrate the inverse relationship between case weight and case volume as shown directly above, these values clearly show up as outliers. In your original graphing approach, they would be spot on a trend line, if one were present, which is misleading because the trend line that is implied by the original scatter plot you showed would have a positive slope. Perhaps it's only my impression and maybe you didn't mean to imply that, but the original graph certainly gave me that impression. Case volume will always show a general decrease (negative slope) as case weight increases, regardless of whether the weight of the case is included or not.